Research
My research primarily involves developing analytical and numerical tools to study quantum information dynamics. However I am interested in many aspects of condensed matter physics, quantum information, and statistical mechanics. Below, I briefly describe the major themes of my current research.
You can find my publications and preprints on Google Scholar, ArXiv or my CV.
Tensor network methods for studying many-body quantum systems
I am interested in using tensor network techniques to study quantum many-body phenomena.
We studied tensor network states on sparse graphs, for which computation of local expectation values are usually difficult due to the presence of loops. We used the belief propagation algorithm to contract tensors on locally tree-like graphs, which allow us to also develop a variational method to approximate ground states of strongly interacting quantum spin models on sparse graphs. [arXiv: 2206.04701]
One aspect of my work has been to study OTOCs by extending known tensor network techniques to study operator dynamics in very large 1D systems and for very long times. This involves bootstrapping the emergent locality of the operator dynamics in the Lieb-Robinson sense with the simple structure of the OTOCs. [Phys. Rev. Lett. 123, 165902 (2019)] [Phys. Rev. B 102, 184303 (2020)]
Measurement-induced entanglement phase transition
Interacting quantum time evolution scrambles hides information from local quantum operations. On the other hand, quantum measurements are inherently non-unitary, and repeated local measurements eventually generate unentangled product states. These two mechanisms can oppose each other, giving rise to the phenomenon of measurement induced phase transition.
We developed analytically solvable large-N Brownian circuits (or time evolutions) for qubits which allow us to derive a mean field model for the measurement-induced phase transition. [Phys. Rev. B 104, 094304 (2021)]
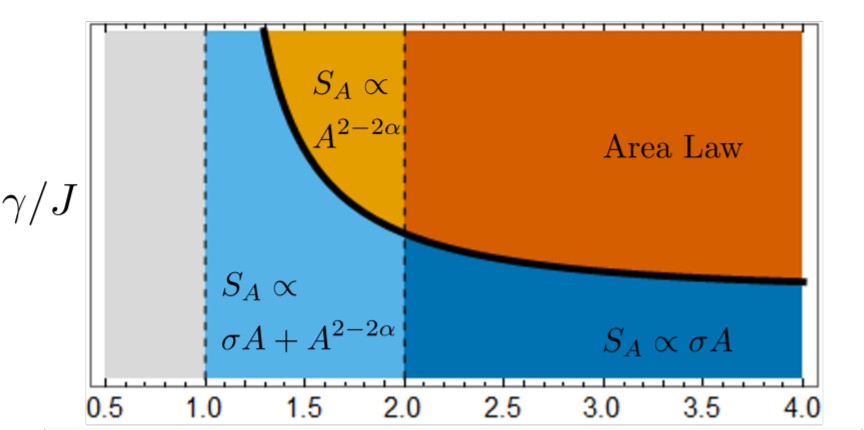
We have also disovered novel measurement-induced entangled phases in the presence of long-range interactions in both spin and fermionic models, by coupling many of the large-N Brownian clusters on lattices with varying connectivities. The long-range interaction develops distinct patterns of entanglement in the states generated by these circuits, improving the quantum-error-correcting properties of the states. [arXiv: 2109.00013]
Quantum Information Scrambling
Scrambling of quantum information refers to the phenomenon by which an isolated quantum system undergoing its inherent quantum dynamics hides initially ‘local’ information in larger and larger subsystems as time passes - generic feature of complex many body dynamics in systems as disparate as cold atoms in a lab and evaporating black hole.
We studied how scrambling is arrested in the presence of quenched disorder in strongly interacting spin systems. By turning up disorder, we scanned the scrambling please diagram across a Thermalization - Many body Localization (MBL) quantum phase transition. We identified a sharp transition in the nature of information scrambling at disorder values lower than the putative MBL transition disorder strengths. [Phys. Rev. Lett. 123, 165902 (2019)]
We numerically studied scrambling in gapped local quantum systems at low temperatures, and discovered non-trivial deviations from the chaos bounds derived by Maldacena, Shenker and Stanford for out-of-time-ordered commutators (OTOC) defined in a particular way. We found that OTOCs depend strongly on the way they are defined at finite temperatures, namely the exact form of the thermal regulation, and only certain specific definitions satisfy the chaos bounds. We also theoretically study the OTOCs in the paramagnetic phase of 2+1 D O(N) non-linear sigma model at low temperatures, and compare the qualitative behavior to what we observe numerically. [Phys. Rev. B 102, 184303 (2020)]